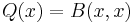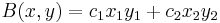Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V (with real or complex scalar field) such that the associated quadratic form
is definite, that is, has a real value with the same sign (positive or negative) for all non-zero x. According to that sign, B is called positive definite or negative definite. If Q takes both positive and negative values, the bilinear form B is called indefinite.
If B(x, x) ≥ 0 for all x, B is said to be positive semidefinite. Negative semidefinite bilinear forms are defined similarly.
Contents |
Example
As an example, let V=R2, and consider the bilinear form
where 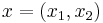 ,
, 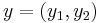 , and
, and 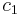 and
and 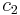 are constants. If
are constants. If 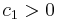 and
and 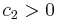 , the bilinear form
, the bilinear form  is positive definite. If one of the constants is positive and the other is zero, then
is positive definite. If one of the constants is positive and the other is zero, then  is positive semidefinite. If
is positive semidefinite. If 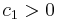 and
and 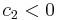 , then
, then  is indefinite.
is indefinite.
Properties
When the scalar field of V is the complex numbers, the function Q defined by 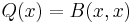 is real-valued only if B is Hermitian, that is, if B(x, y) is always the complex conjugate of B(y, x).
is real-valued only if B is Hermitian, that is, if B(x, y) is always the complex conjugate of B(y, x).
A self-adjoint operator A on an inner product space is positive definite if
- (x, Ax) > 0 for every nonzero vector x.
See also
References
- Nathanael Leedom Ackerman (2006) Lecture notes Math 371, Positive definite bilinear form is definition 0.5.0.7, weblink from University of California, Berkeley.